Aspects énergétiques des systèmes mécaniques

(chapitre 13 de physique)

Introduction : Quels sont les différentes formes d’énergie présentes dans les systèmes mécaniques ?

   I°) Rappel de 1°S :

     1°) Travail d’une force constante :

      Le travail d’une force constante  dont le point d’application se déplace de A à B sur le segment [AB]  est égal au

     produit scalaire du vecteur force  par le vecteur déplacement. On note :

      W_AB() =…………………=……………………………. avec   * W_AB() travail de la force en ……………..

     * F : valeur de la force en …………………….

     *AB : longueur du déplacement en  ………

      * a : angle entre les vecteurs  et …………..

      Schéma :

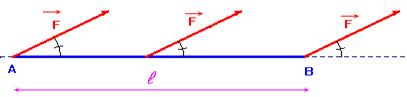
  Le travail est une grandeur algébrique  :

    si 0<a<90 alors ……………..et W_AB()……. ….. le travail est …………..

    si a=90  alors ……………...et W_AB()……….. le travail est …………………( ……… à ………..)

    si 90°<a<180° alors …………..et le travail est …………………

    2°) Travail du poids d’un corps :

          Considérons un solide S de masse m et de centre d'inertie G se déplaçant dans un champ de pesanteur

           uniforme .

      La définition du travail mécanique d'une force constante s'applique dans ce cas :

      W_AB() =………………..………=…….………………………….

    Schéma :

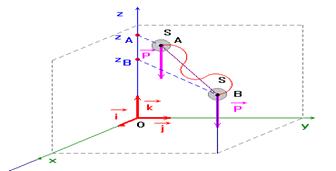
    Dans le repère choisi, on peut exprimer les coordonnées de chaque vecteur :

       En conséquence : W_AB()= ….…………………..…... =…………………………..…

       Le travail du poids d'un corps transféré à un objet ne dépend que de la …………………………………………..………

       de son centre d'inertie.

  3°) Travail élémentaire d’une force non constante :

      Pour calculer le travail d’une force variable, on découpe le trajet en trajets élémentaires suffisamment petits pour

      considérer que la force est constante sur chacun des déplacements élémentaires. Par définition, le travail élémentaire

     de la force  pour le déplacement élémentaire est donné par la relation : W () =

     Pour obtenir le travail de la force variable , sur le trajet de A à B, on fait la somme de tous les travaux élémentaires :

     W_AB()=W ()=…………………………..

     Le travail d’une force quelconque  entre A et B le long d’un trajet quelconque est égal à la somme de tous les travaux

      élémentaires entre A et B.  Si le déplacement devient infiniment petit, on a qui peut s’écrire …………….dans ce cas le

      travail ci-dessus correspond à :

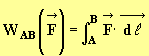
4°) Travail de la force appliquée à l’extrémité d’un ressort :°

   La force appliquée à l’extrémité d’un ressort par un opérateur (l’autre extrémité étant fixe) est appelée ……………..du ressort.

  La tension du ressort . Avec O  position de l’extrémité du ressort à vide et M position de l’extrémité du ressort

   lorsqu’il est déformé.

   On prend l’axe x’Ox pour repérer l’allongement algébrique :

 Calculons le travail de la tension du ressort pour passer de de x _A à  x _B :

Comme l’allongement passe de x _A à  x _B, la force varie au cours du déplacement. Le travail se calcule en cherchant

 l’expression du travail élémentaire effectué par la force pour passer de l’allongement x à l’allongement x + dx :

 : W () ==……..............................=……………………..si l’allongement  devient très petit on peut écrire :

   (travail élémentaire)= …………………=……………………….

   Par intégration, on obtient le travail de la tension du ressort pour passer de l’allongement x _A à l’allongement x _B :

       W_AB()=()=………………………….= …………………………=………………….……………..

II°) Energie potentielle de pesanteur :

  1°) Notion d’énergie potentielle :

  C’est la forme d’énergie que possède un système du fait de sa position par rapport au système avec lequel il est en

   interaction.

   Exemples : l’énergie potentielle de  …………………………… et l’énergie potentielle élastique.

2°) Énergie potentielle de pesanteur :

   L’énergie emmagasinée par un corps du fait de sa position par rapport à la Terre est appelée énergie potentielle de

   pesanteur.

    l’énergie potentielle de pesanteur augmente avec……………..…….. Il faut choisir une altitude de référence qui

    simplifie les calculs.

    Ainsi l’expression de l’énergie potentielle de pesanteur d’un solide S situé à l’altitude z (par rapport à l’altitude de

    référence) est :

E_PP=…………………………..  (avec   * E_PP énergie potentielle de pesanteur en ……………..

                                                                                                                                 * m : masse en …………………….

 *g : intensité de pesanteur en …………….

 * z : altitude du centre d’inertie en …………..

3°) Énergie potentielle élastique :

  L’énergie potentielle élastique, que possède un ressort qui est allongé ou détendu, est définie par la relation suivante :

   E_Pe=kx²   avec  * E_Pe énergie potentielle élastique  en ……………..

     *k : constante de raideur en …………….

     * allongement algébrique du ressort en mètre

III°) Energie mécanique d’un système :

1°)  Énergie cinétique de translation :

  L’énergie cinétique de translation d’un système, de masse m et de vitesse v, dans un référentiel donné, est donnée par la

  relation :

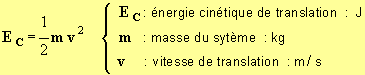
       2°) Energie mécanique d’un système { solide + ressort } horizontal) :

    L’énergie mécanique  E_m du système S = {solide + ressort } horizontal est la somme de l’énergie cinétique E_C du système

     S et de l’énergie potentielle élastique E_pe du ressort.

    E_{m=……………………………………………=………………………………………………..}

   Remarques : l’énergie mécanique du système S se conserve si le système évolue sans frottement. Dans ce cas

  E_m1 (position 1) =E_m2 (position 2)= …………………………………………………………

  Dans le cas contraire, le système cède de l’énergie au milieu extérieur. Son énergie mécanique diminue au cours

   du temps. La variation d’énergie mécanique est égale au travail des forces de frottement qui s’exercent sur le

   système :

 E_m = W < 0.

                                 Au cours des oscillations, l’énergie cinétique (partie mobile) du système se transforme en énergie potentielle

 élastique (ressort) et réciproquement. Pour l’élongation maximale on a que de l’énergie …………………………..

 pour la position d’équilibre on a  que de l’énergie ………………………….. Entre ces deux positions on a un

 mélange de ces deux formes d’énergies pour le système S.

     3°) Énergie mécanique d’un projectile :

     L’énergie mécanique d’un projectile dans un champ de pesanteur uniforme est la somme de son énergie potentielle de

     pesanteur et de son énergie cinétique dans le référentiel d’étude.

    E_m=………………………………..=…………………………………

  Remarques : Si le mouvement s’effectue sans frottement, l’énergie mécanique se conserve :

E_m1 (position 1) =E_m2 (position 2)= ……………………………………………………………

Dans le cas contraire, le système cède de l’énergie au milieu extérieur. Son énergie mécanique diminue au cours du temps. La variation d’énergie mécanique est égale au travail des forces de frottement qui s’exercent sur le système :

 E_m = W < 0.

Si le projectile s’élève, son énergie …………………..…..se transforme en…………………………………………...

Quand le projectile descend, son énergie ………………………..de pesanteur se transforme en……………………