Les oscillations libres d'un circuit R,L,C
(chapitre 9 de Physique)
Introduction : Le circuit du tuner d’une chaîne stéréo permettant de sélectionner une station radio est constitué d’un système
oscillant modélisé par une bobine branchée aux bornes d’un condensateur. Pourquoi et comment un circuit peut-il être le siège
d’oscillations ?
I°) Rappels :


a°) Utilisation de l'ordinateur pour visualiser la décharge oscillante d'un condensateur :
|
décharg
|

Représenter sur le schéma ci-dessus les branchements de l'oscilloscope qui permettent de visualiser uG sur la voie B
et uC sur la voie c .
Le montage en TP a été réalisé avec une bobine a inductance réglable L et de résistance r d’environ = 10 W.
On a pris L = 1 H. On prend une boite de condensateurs. On prendra C = 10 mF. R est une boite de résistances.
On prendra R = 0 W.
Dessiner l'oscillogramme obtenu sur la voie C .
![]() Interprétations:
Interprétations:
La tension aux bornes du condensateur à t = 0 s vaut……, le condensateur a emmagasiné une énergie Ec = ½ CE2.
Le condensateur donne son énergie à la bobine ; puis la bobine ……………………………………………au condensateur.
On appelle oscillations libres les variations de tension aux bornes du condensateur.
Ces dernières sont amorties : la tension max décroît au cours du temps car il y a perte d’énergie par ……………..(lié à la
résistance r de la bobine).
b°) Influence des différents facteurs :
Expérimentalement nous avons montré que la pseudo-période était indépendante de la ………………………….
Par la suite nous avons fait varier C et L :
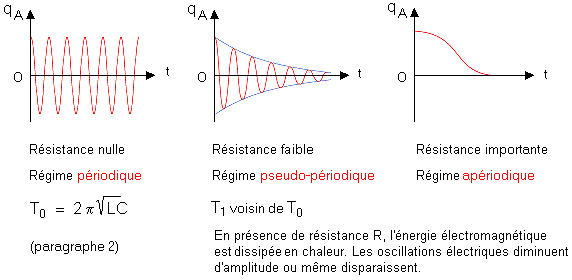
Définitions : Pseudo – période :
c’est la durée T entre deux valeurs de Uc = OV , la tension
variant dans le même sens
|
|
Si la bobine n’avait
pas du tout de résistance les oscillations ne seraient pas ………………………. On ne parlerait plus
de pseudo -période mais de période propre. Cette période propre
(sans amortissement) est donnée par la formule :
To=2p
|

C (mF) |
10 |
1 |
10 |
L (H) |
1 |
1 |
0,5 |
Texpérimental ( ms) |
..... |
..... |
..... |
TO= 2p.
|
..... |
..... |
..... |
CONCLUSION : lorsque l’amortissement est faible, la pseudo-pèriode T est ……………………….. à la période propre
TO d’un circuit L,C sans résistance.
|

Nous choisissons C =10 mF et L = 1 H et nous faisons faire varier R entre 0 et 300 W (de 50 W en 50 W).
Remarque : En présence de résistance, on peut néanmoins entretenir des oscillations électriques d'amplitude constante
avec un montage à amplificateur opérationnel. Ce montage est chargé de redonner au circuit R, L, C l'énergie consommée
dans la résistance R par effet Joule;
Il existe une résistance particulière notée Rc qui délimite le régime pseudopériodique d’apériodique : on parle de régime critique
(Rc : résistance critique) : Rc= …………….
III°) Etude théorque du circuit (R)L,C :
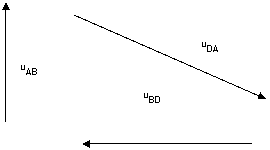
| uBD |
| uDA |
| uAB |
 a°) Circuit R,L,C :
a°) Circuit R,L,C :
|
uAB + uBD + uDA =0 ou uC +uR +uL=0 ce qui s'écrit encore : ………………………= 0 ……………………….=0
Ceci est l’équation différentielle vérifiée par la charge q du condensateur.
|
|
b°) Etude théorique des oscillations d'un circuit série LC d'amortissement négligeable (R=0 W) :
1) Tension aux bornes du condensateur :
On respecte la convention récepteur u et i de sens contraire.
uL = L.di/dt ; q = C.uC ; i = dq/dt = C.duC/dt
Loi des tensions : uL + uC = 0
L.C.d2uC/dt2 + uC
= 0 ou d2uC/dt2 + uC /(L.C)=
0
(on peut aussi écrire une équation différentielle pour q)
La solution de l'équation différentielle précédente est : uC = Um.cos (ω0.t+ φ0)
Um, ω0 et φ0 étant des constantes à déterminer.
duC/dt = -ω 0.Um.sin(ω0.t+φ0) ; d2uC/dt2 = - ω02.Um.cos(ω0.t+φ0)
d2uC/dt2 + uC/(L.C) = (-ω 02 + 1/(L.C)).Um.cos(ω0.t+φ0) = 0 . Relation valable pour tout t.
Il faut donc : - ω02.+
1/(L.C) = 0 soit ω 0
= 1/![]()
ω0 est appelée
pulsation propre des oscillations électriques , elle s'exprime en rad.s-1
On utilise les conditions initiales pour déterminer Um et φ0:
à t = 0 s , uC = Um.cos(φ0) ; φ0est
appelé phase à l'origine . Souvent uC = Um , φ0=
0
La fonction cosinus varie entre –1 et 1, Um est donc la valeur
maximale, appelée amplitude de uC dans ce cas Um = E
On appelle T0, la période propre des oscillations électriques :
T0 = 2 π/ ω
0 = 2π .![]()
T0 s'exprime en s. Dans un régime pseudo-périodique, la pseudo-période est proche de T0
La fréquence propre f0 ( ou N0 ) : f0 = 1 / T0
Analyse dimensionnelle :
[L.C] = [L / R].[RC] ; or [t] =[RC] = T et [t] = [L / R] = T donc [L.C] = T2
d'où [![]() ]
= T ;
]
= T ; ![]() a
bien la dimension d'un temps
a
bien la dimension d'un temps
2) Intensité du courant :
i = dq/dt ; q = C.uC = C. Um.cos (ω0.t+φ0
)
donc i = - C.Um.ω0.sin(ω0.t+φ0)
a°) Cas du circuit R,L,C (résistance non nulle) :
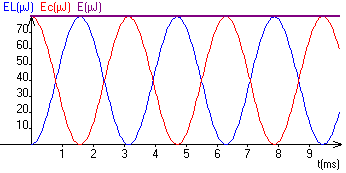
| EL: énergie magnétique emmagasinée par la bobine: EL=1/2Li2 | |
| EC: énergie électrique emmagasinée par le condensateur: EC=1/2Cuc2 | |
| E: énergie totale emmagasinée par le circuit: E = EL + EC |
On peut ainsi tracer les courbes donnant ces énergies en fonction du temps.
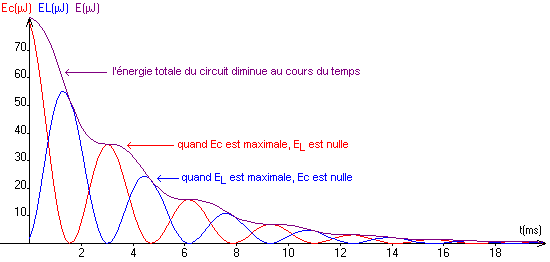
Conclusions:
| L'énergie totale du circuit E décroit au cours du temps: E est progressivement dissipée par effet Joule dans le conducteur ohmique. | |
| L'énergie emmagasinée par le condensateur est maximale quand l'énergie emmagasinée par la bobine est nulle et vice versa. | |
| Il y a transfert d'énergie entre le condensateur et la bobine. |
b°) Dans le cas d'un régime périodique (résistance du circuit nulle), l'énergie totale est constante.