La lumière : modèle ondulatoire (chapitre 4 de physique)
Introduction : Exposés en pleine lumière, des CDROMS présentent des reflets irisés. Comment expliquer ce phénomène ?
I°) Le modèle ondulatoire de la lumière :
1°) Diffraction de la lumière
Réalisons l'expérience suivante (réalisée au TP N°6):

figure de diffraction obtenue 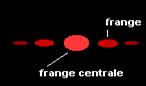 sur
l’écran
sur
l’écran
Laser fente
Écran
On observe sur l'écran une figure de diffraction. (tache principale et d’autres taches sur les côtés). Ce phénomène se
produit lorsque l'ouverture par laquelle passe la lumière est de petite taille. On dit que l'ouverture a diffracté
la lumière du laser.
Remarques:
· Plus l'ouverture est petite (proche de l source(laser)) , plus le phénomène de diffraction est marqué.
· Le phénomène de diffraction met en évidence le fait que l’on ne peut résumer la lumière par une droite avec une flèche
(principe de propagation de la lumière en ligne droite dans un milieu homogène et transparent.).
2° ) Interprétation ondulatoire
De façon générale, la lumière peut-être considérée comme une onde électromagnétique. En particulier, la lumière émise
par le laser peut-être décrite comme une onde électromagnétique sinusoïdale de fréquence donnée. Cette onde subie des
déviations lorsqu’elle rencontre une ouverture ou un obstacle de petites dimensions (proche l source(laser).)
La lumière se propage dans le vide, et dans les milieux transparents (air, eau, gaz, verre, etc...).
Dans le vide, la célérité de la lumière est c = 299 792 458 m.s-1 (on
retiendra c ![]() 3,00.108
m/s).
3,00.108
m/s).
Remarques: La célérité de la lumière dans le vide ne dépend pas de la fréquence de l'onde.
La célérité
de la lumière dans l'air est pratiquement égale à sa célérité dans le vide (cair ![]() cvide).
cvide).
II°) Couleur et longueur d'onde :
1°) Lumière monochromatique :
Définition : On appelle lumière monochromatique une onde électromagnétique progressive sinusoïdale de
fréquence donnée.
La couleur de cette lumière est liée à la valeur de sa fréquence (en Hz). Ce qui revient à dire qu’à une radiation
correspond une et une seule fréquence. Cette dernière est indépendante du milieu de propagation, elle ne
caractérise que la source lumineuse. Le spectre du visible s’étale du violet (7,50´1014 Hz) au rouge (3,70´1014 Hz)
(voir livre p 69)
2°) Longueur d'onde :
Comme toutes les ondes périodiques, les ondes électromagnétiques présentent une double périodicité (temporelle
(caractérisée
par T ou f
) et spatiale.
La périodicité spatiale correspond à longueur d'onde
dans le vide , elle sera notée lo.
On l’obtient grâce à
la formule :
lo= C.T=C/f (attention avec C=célérité dans le vide).
Le
spectre du visible dans le vide s’étale donc de
lo
violet (
3,00.108/7,50.1014![]() 400
nm)à
lo
rouge (3,00.108/7,50.1014
400
nm)à
lo
rouge (3,00.108/7,50.1014
![]() 800
nm )
800
nm )
III°) Propagation d'une onde lumineuse dans un milieu transparent :
1°) Indice de réfraction
Remarques préliminaires
·
La
célérité d'une onde électromagnétique dépend du milieu de propagation. (vdiamant ![]() 1,2´108
m/s
1,2´108
m/s
veau ![]() 2,3´108
m/s voir livre p 69)
2,3´108
m/s voir livre p 69)
· La célérité d'une onde électromagnétique dans un milieu transparent est toujours inférieure à la célérité de
c ette onde dans le vide (c).
Ces 2 remarques se retrouvent dans la définition ci-dessous
Définition : L'indice de réfraction d'un milieu transparent est le rapport entre la célérité d'une onde se propageant dans le
vide (c)
et sa célérité dans le milieu considéré (v).
|
avec |
|
n: indice de réfraction du milieu transparent |
|
|
c: célérité de l'onde dans le vide (3.108m.s-1) |
||||
|
v: célérité de l'onde dans le milieu transparent (m.s-1) |
n diamant ![]() 3,00.108/
1,2´108
3,00.108/
1,2´108 ![]() 2,5 n eau
2,5 n eau ![]() 3,00.108/
2,3´108
3,00.108/
2,3´108
![]() 1,3
1,3
2°) Indice et longueur d’onde :
La longueur d’onde d’une radiation dans un milieu quelconque (de célérité v) se calcule de la façon suivante :
l= v.T=(c/n).T=l vide/n
Ex : llaser
(vide ou air) ![]() 633
nm (633.10-9 m)
l
laser (eau)
633
nm (633.10-9 m)
l
laser (eau) ![]() 633/1,3
633/1,3 ![]() 486 nm
.
486 nm
.
Comme pour les ondes mécaniques, la fréquence et la période sont les seules caractéristiques d’une onde
lumineuse (indépendant du milieu de propagation). Par contre la longueur d’onde d’une radiation change quand
on change de milieu.
IV°) Dispersion de la lumière blanche :
1°) Milieu dispersif - milieu non dispersif
Définition: Un milieu transparent est dit dispersif si la célérité d'une onde lumineuse monochromatique qui se propage
dans ce milieu dépend de sa fréquence.
Définition: Un milieu transparent est dit non dispersif si la célérité d'une onde lumineuse monochromatique
qui s'y propagene dépend pas de sa fréquence c’est le cas pour l'air ou le vide.
2°) Rappels des lois de la réfraction :
La réfraction correspond au changement de direction d’une onde lumineuse quand elle passe d’un milieu
homogène à l’autre.

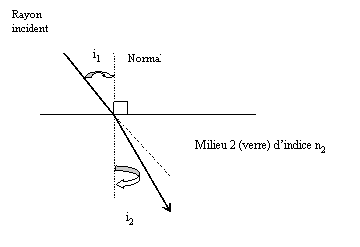
Cas ou n2>n1 (passage de l’air dans le verre par exemple)
|
Milieu 1(air) d’indice
n1 |
|
Milieu 2 (verre)
d’indice n2 |
|
Rayon incident |
|
i2 |
|
i1 |
|
Normale |
|
Rayon réfracté |
3°) Dispersion de la lumière blanche :
Expérience : on envoie une lumière blanche c'est-à-dire polychromatique (composée de plusieurs ondes monochromatiques
de fréquences différentes) à travers un prisme . On observe un spectre avec toutes……………………………………………
Le violet étant la couleur la plus ………………… et le rouge la ………………………………
Interprétations : la 2° loi de DESCARTES s’applique à toutes les radiations : nair´sin i1=nverre´sini2
L’angle d’incidence i1 est le …………………….. quelque soit la radiation (toutes les radiations se superposent au départ
pour former du blanc). nair est le même quelque soit la radiation (le vide et l’air ne sont pas des milieux ………………………).
Par conséquent nairx sin i1 =……………… quelque soit la radiation. Ce qui implique nverrexsini2= ………………. or i2 varie
(voir dessin ci-dessous), donc pour garder nverrexsini2=cst cela induit que l’indice du verre n’est pas …………………donc
il varie avec la ………………………………………………..

Conclusion : L’indice d’un milieu transparent et homogène (autre que l’air) varie avec la radiation lumineuse.
Ce qui revient à dire que la vitesse de propagation d’une radiation lumineuse dans un milieu (autre que l’air
ou le vide) dépend de la fréquence de l’onde qui s’y propage : c’est le phénomène de ……………………………
V°) Retour sur le phénomène de diffraction :
L
|
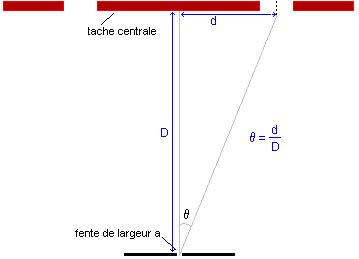
Lorsqu’un faisceau parallèle de lumière monochromatique (type laser) de longueur d’onde dans le vide (ou l’air) l0 traverse une fente de largeur a, l’écart an gulaire entre le milieu de la tache centrale et la première extinction est donnée par la
relation :
q(rad) =........................Pour
des petits angles (en radian) tg
q=……….=……..….»
q
Ce qui donne
l0
»La/2D
avec L : largeur de la tache centrale
en mètre
a :
largeur de la fente en …………..
D :
distance entre la fente et l’écran en ……
|
