Les ondes mécaniques progressives et périodiques (chapitre 3

de physique)

 

Introduction : Une note de musique obtenue avec un diapason est une onde mécanique progressive  périodique.

                          Comment  caractériser ce type d’onde ?

 

 I°) Définition :

Une onde mécanique est progressive si elle se propage depuis un point source dans tout le milieu matériel .Elle est périodique si la perturbation se répète de façon identique au cours du temps  ; c’est un mouvement vibratoire entretenu  (vagues de la houle, la d’un diapason, ondes sur une cuve à onde….)
Zone de Texte: Une onde mécanique est progressive si elle se propage depuis un point source dans tout le milieu matériel .Elle est périodique si la perturbation se répète de façon identique au cours du temps  ; c’est un mouvement vibratoire entretenu  (vagues de la houle, la d’un diapason, ondes sur une cuve à onde….)

 

 

 

 

II°) Onde mécanique périodique sinusoïdale :

        a°) Périodicité temporelle (période) :

Définition: La période d'un phénomène périodique est la durée au bout de laquelle le phénomène se répète à lui-même. On la note T et elle s'exprime en seconde (s).

 

Définition: La fréquence d'un phénomène périodique représente le nombre de phénomènes effectués par seconde. On la note généralement f, son unité est le hertz   (Hz). La fréquence est l'inverse de la période :
 

 f=1/T

   avec     

f: fréquence du phénomène en hertz (Hz)
 

T: période du phénomène en secondes (s)

 

 
Zone de Texte: Définition: La période d'un phénomène périodique est la durée au bout de laquelle le phénomène se répète à lui-même. On la note T et elle s'exprime en seconde (s).   Définition: La fréquence d'un phénomène périodique représente le nombre de phénomènes effectués par seconde. On la note généralement f, son unité est le hertz   (Hz). La fréquence est l'inverse de la période :    f=1/T   avec      f: fréquence du phénomène en hertz (Hz)   T: période du phénomène en secondes (s)    

 

 

 

 

 

 

 

 

   

 

           Pour définir la période ou la fréquence d’une onde mécanique progressive sinusoïdale on utilise un stroboscope.

 

 

      b°) Principe de la stroboscopie :


Le disque fait un tour complet entre deux éclairs

 

Soit Te la période des éclairs du stroboscope.

Si Te=k.T (avec k entier naturel), l'objet semble  immobile

 

 

Remarques : - La valeur la plus faible de la période (ou la plus grande des fréquences) des éclairs qui

                         donne l'immobilité apparente  est égale à la période  du   phénomène : T éclair= T phénomène périodique

- Quand T éclair< T phénomène périodique alors le phénomène périodique va au ralenti en sens inverse

- Quand T éclair>T phénomène périodique alors le phénomène périodique va au ralenti dans le même sens

 

III°) Onde progressive périodique à une dimension:

         1°) Etude expérimentale :

            Soit une source S (extrémité d’une scie sauteuse) imposant une perturbation périodique sinusoïdale

            au milieu de propagation   (corde).

            On constate qu'une onde progressive périodique se propage dans le milieu.
       

 

       2°)  Périodicité temporelle

 

  

Représentation spatiale de la corde

Ci-joint (à droite) , l'aspect de la corde à un instant donné. L'élongation de la source et d'un point M quelconque est en général différente, mais on peut remarquer une périodicité dans le mouvement de chaque point de la corde.

  

Représentation temporelle du point S

  

Représentation temporelle du point M

 

L'élongation de la source S est périodique de période T. C'est une fonction sinusoïdale du temps.

  

L'élongation du point M est elle aussi périodique de même période T.

    La période du mouvement de chaque point de la corde est imposée par la  

    source S. 

 

 

3°) Périodicité spatiale

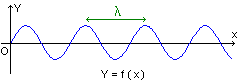
   L'aspect de la corde à un instant donné est une fonction sinusoïdale de

  l'abscisse x de chacun des points du milieu.

 

     Définition: On appelle longueur d'onde (notée   l) la période spatiale de l'onde

                  progressive périodique.

 

 

L'onde présente donc une double périodicité:

bullet une périodicité temporelle de période T (exprimée en secondes).
bullet une périodicité spatiale de période l (exprimée en mètres).

 

 

       4°) Relation entre période et longueur d'onde

 

 

 

 

La longueur d'onde est la distance parcourue par l'onde pendant une

  durée égale à une période
 

l = v*T=V*1/f

 

  avec

  

 l en mètres

v en m/s

T en secondes

f en Hz

Remarques : - l varie avec la fréquence si on garde le même milieu de propagation (donc même vitesse).

                        - si on change de milieu de propagation (donc de vitesse

 ), pour la même fréquence, l varie.

 

 

Remarques:

l/2
Zone de Texte: l/2   

l/2
Zone de Texte: l/2  

3l/2
Zone de Texte: 3l/2

 

3l/2
Zone de Texte: 3l/2

- Les points M, M' et M'' conservent la même élongation quelque soit l'instant t. On dit que les points M, M' et M'' vibrent en phase,

   dans ce cas 2 points qui vibrent en phase sont séparés par une distance d= k*l (avec k entier ).

 

- Les points A  et C ainsi  que B et C ont des élongations opposées quelque soit l'instant t. On dit que les points A et C ainsi que B et

   C vibrent en opposition de  phase, dans ce cas 2 points qui vibrent en opposition  de phase sont séparés par une distance

 d= (2k+1)* l /2 (avec k entier ).

 

 
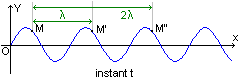
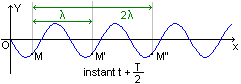
Zone de Texte: - Les points M, M' et M'' conservent la même élongation quelque soit l'instant t. On dit que les points M, M' et M'' vibrent en phase,    dans ce cas 2 points qui vibrent en phase sont séparés par une distance d= k*l (avec k entier ).   - Les points A  et C ainsi  que B et C ont des élongations opposées quelque soit l'instant t. On dit que les points A et C ainsi que B et    C vibrent en opposition de  phase, dans ce cas 2 points qui vibrent en opposition  de phase sont séparés par une distance  d= (2k+1)* l /2 (avec k entier ).    

 

 

 

 

 

 

 

 

 

 

IV) Cas des ondes à deux ou à trois dimensions :

        1°) Ondes à la surface de l'eau

 

 

Ondes circulaires

 

Les points M1 et M2 vibrent en phase si |d2-d1| = kl.

 

 

 

 

Ondes rectilignes

Les points M1 et M2 vibrent en phase si d = …..

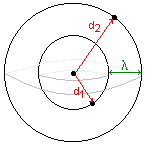     2°) Ondes sonores

       Les points M1 et M2 vibrent en phase si |d2-d1| = k.l (voir image ci-contre).

 

 

 

 

 

V°) Diffraction et dispersion :

     1°)  Diffraction d'une onde progressive sinusoïdale

        Soit une onde plane périodique (réalisée avec une cuve à onde)  rencontrant un obstacle ou une ouverture.

  

 

Cas n°1
L'ouverture est de grande taille par rapport à la longueur  d'onde
(l négligeable par rapport à a).

Cas n°2
L'ouverture est de petite taille par rapport à la longueur d'onde
(l non négligeable par rapport à a).

 

    Dans le cas n°2, l'onde change de direction et de comportement sans changement de sa longueur d'onde: elle est

    diffractée (le phénomène mis en évidence s'appelle la diffraction).

Définition : Une  ouverture (ou un obstacle) interposé sur le trajet d’une onde progressive, se comporte comme une source secondaire. Cette dernière émet dans toutes les directions, et à la même fréquence que la source primaire (même longueur d’onde , même vitesse) : c’est le phénomène de diffraction. Plus la longueur de  l’ouverture (a) se rapproche de la longueur d’onde de la source l,  plus ce phénomène sera important.

 
Zone de Texte: Définition : Une  ouverture (ou un obstacle) interposé sur le trajet d’une onde progressive, se comporte comme une source secondaire. Cette dernière émet dans toutes les directions, et à la même fréquence que la source primaire (même longueur d’onde , même vitesse) : c’est le phénomène de diffraction. Plus la longueur de  l’ouverture (a) se rapproche de la longueur d’onde de la source l,  plus ce phénomène sera important.    

 

 

 

 

 

 2°) Dispersion d'une onde (activité réalisé à partir de clichés pris sur une cuve à onde) :

1°) Mesurer la longueur d’onde moyenne pour les 4 clichés.

2°) Calculer la vitesse correspondante dans chaque cas.

3°) Conclure

Définition: Un milieu est dit dispersif si la célérité des ondes qui se propagent dans ce milieu varie avec la fréquence.

 
Zone de Texte: Définition: Un milieu est dit dispersif si la célérité des ondes qui se propagent dans ce milieu varie avec la fréquence.    

 

 

 

        L’eau est un milieu dispersif  (voir activité ci-dessus). L’air n’est pas un milieu dispersif pour les ondes sonores.

        Les aiguës (hautes fréquences) et les graves (basses fréquences) parviennent simultanément à notre oreille.

        Ce constat n’est   plus vrai quand les amplitudes sonores sont très élevées : le roulement du tonnerre correspond à l’arrivée

        tardive des basses  fréquences  (sons graves).