Les systèmes oscillants

Les systèmes oscillants (chapitre 12 de physique : 1ère partie)

Introduction : Une balançoire est un système oscillant, quelles sont les grandeurs physiques qui régissent la période propre de

ce pendule.

I°) Définitions :

1°) Oscillateur mécanique : Un oscillateur mécanique est un système animé d'un mouvement de………………….., en général

autour d'une position d'équilibre stable.

C'est par exemple le cas d'une …………………………………………………………………………………………………

2°) Pendule pesant ( Cas particulier du pendule simple) :

- Un pendule pesant est un solide qui oscille autour d'un axe fixe, de part et d’autre de sa position de repos sous l’action de

son ………….................

- Un pendule simple est constitué d’un solide de petites dimensions, de masse m, suspendu à un point fixe O par un fil

inextensible de longueur L, de masse négligeable. Ecarté de sa position d’équilibre, il oscille dans le champ de pesanteur

terrestre g.

II°) Etude des oscillations libres non amorties du pendule simple :

Considérons un pendule simple constitué d’une petite bille de masse m, suspendue à un fil de longueur L.

1°) Etude théorique du mouvement du pendule simple :

Les oscillations sont dites libres car le pendule, écarté de sa position d'équilibre (il reçoit alors de l'énergie potentielle),

est………………………………………….... Elles sont non amorties lorsqu'on peut négliger les……………………….

Référentiel Galiléen : …………………..

Système étudié : …………………………….

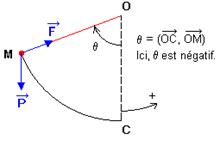
Deux forces appliquées : Le poids et la force (action du fil sur la bille)

Appliquons la deuxième loi de Newton (ou principe fondamentale de la dynamique) :

Dans un référentiel Galiléen, la somme des forces extérieures appliquées à un solide est égale au produit de la masse du solide

par l'accélération de son centre d'inertie :

Ici, on écrit : …………………………………………………………………………………..

L'étude détaillée de cette équation n'est pas au programme. Remarquons simplement que seul le vecteur est constant. Le

vecteur ………………………………. par conséquent le vecteur accélération …………………. durant le mouvement.

Position d'équilibre : A l'équilibre ………………………... Le vecteur est toujours vertical et dirigé vers le bas.

Par conséquent, à l'équilibre, le vecteur ……………………….doit être vertical et dirigé vers le haut. La position d'équilibre du

pendule est donc la position……………………….

Remarques : Oscillation : Une oscillation correspond au trajet effectué par le solide entre deux passages consécutifs par la

…………………………………………………………………………………………………………………....................

Amplitude a_m : L'amplitude des oscillations est la valeur maximale a _m de l’angle défini par le pendule à sa position

la plus élevée par rapport à la …………………...........

Période propre To : La période propre To des oscillations non amorties du pendule est la durée séparant

…………………………………………………………………………………………………………….

2°) Etude expérimentale de la période d'un pendule simple en fonction des différents paramètres (Tp dirigé de physique) :

a°) Le professeur lance simultanément, à partir d'un même angle a₀ , trois pendules simples (même longueur de fil) mais

trois boules différentes (même diamètre mais masse différente) et on observe leurs mouvements. Observer.

b°) Etudier l'évolution de la période T en fonction de l'amplitude angulaire maximale (faire 3 mesures de la période avec

des angles de départ de 10°, 15° et 50°).

c°) Modifier la longueur du pendule et mesurer la nouvelle période.

Résultats et exploitation des mesures.

Les résultats sont donnés, vous devez en faire leur exploitation:

a°) exploitation de a°):

Pendant un temps assez long, les trois pendules oscillent………………………………….., ce n'est qu'après une dizaine

d'oscillations que l'on peut constater un écart.

Conclure : …………………………………………………………………...................................................................................................

………………………………………………………………………………………………………………………………...........................

…………………………………………………………………………………………………………………………………............................

b°) exploitation de b : influence de l'amplitude des oscillations:

On mesure la durée de 5T seulement pour conserver l'amplitude constante car au delà, l'amortissement est perceptible et

a maximale décroît à chaque période.

Avec l = 0,50 m et une boule de plomb, nous obtenons pour différentes valeurs de a₀ :

a₀	5	10	15	20	25	30	40	50
5T(s)	7,1	7,1	7,1	7,15	7,2	7,2	7,3	7,4
T(s)	……	…….	…….	……	……	……	……	……

Conclusion : Isochronisme des petites oscillations du pendule simple : …………………………………………..........................

………………………………………………………………………………………………………………………………...........................

………………………………………………………………………………………………………….....

c°) exploitation de c :

Pour différentes longueurs de l on mesure la durée de 5 périodes pour une petite amplitude de départ (inférieure à 10°).

La longueur du pendule est égale à la longueur du fil augmentée du rayon de la boule.

l(m)	1,20	1,00	0,80	0,60	0,40	0,20
5T(s)	11,0	10,05	8,90	7,75	6,45	4,50
T(s)	……...	……...	……...	……...	……...	……...

Construire le graphique représentatif de T² = f(l)

Comparer le coefficient directeur de la droite à 4Π²/g.

Conclusion lorsque la période est indépendante de l’amplitude de départ (pour des petits angles) ce qui revient à négliger les

………………………… on a quasi des oscillations libres non amorties. Dans ce cas la période qui ne dépend que des paramètres

………………………….. est appelée période propre du pendule simple notée T₀. L’expression de la période propre de ces petites

oscillations est : To= avec …… en mètre (m) et …………. en N/kg ou ………………

On remarque que la période propre des petites oscillations du pendule simple est indépendante de sa ………………...

III°) Oscillations libres amorties :

En réalité, existent toujours des forces de frottement qui dissipent de la chaleur vers le milieu extérieur et font diminuer l'énergie du

pendule placé dans le champ de pesanteur terrestre. Cela se traduit par une diminution de …………………….. des oscillations.

Cette diminution de l'amplitude existe déjà dans l'air mais devient très visible si le pendule oscille dans de l'eau ou mieux dans de

l'huile très visqueuse.

Dans le premier cas (amortissement faible dans l'eau) le régime est dit pseudo-périodique.

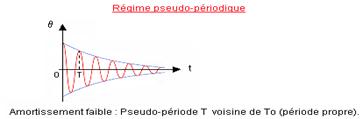
La pseudo-période T des oscillations amorties du pendule est la durée séparant deux passages successifs de l'oscillateur par

…………………………………………………... Si l'amortissement est faible T est voisin de la………………………....................

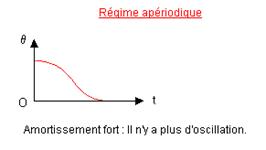
Dans le deuxième cas (amortissement important dans de l'huile très visqueuse), la bille, écartée de sa position d'équilibre puis

lâchée, revient vers cette position d'équilibre sans la dépasser. On dit que le régime est apériodique.