Les lois de Newton (chapitre 10 de physique)
Introduction : La technique d’un golfeur permet de maîtriser les conditions initiales (a , Vo) du mouvement de la balle.
Les lois de Newton font le reste.
I°) Quelques rappels de cinématique :
Définitions :
Remarque : le repère d'espace lié à un référentiel, est souvent un système d'axes orthogonaux et normés, muni d'une origine
O. Dans ce repère, on peut exprimer les coordonnées du mobile ponctuel étudié.
L'étude du mouvement d'un mobile nécessite non seulement le choix d'un référentiel auquel on associe un repère
mais encore le choix d'une horloge (origine des temps) permettant de mesurer le temps.
II°) Le vecteur vitesse :
1°) Définitions :
a°)
Vecteur position d'un mobile ponctuel
Dans le repère orthonormé, lié au référentiel d'étude la position d'un mobile ponctuel est, à l'instant t, donnée par le
vecteur position :
(t)
= x (t) + y (t) + z (t)
A cet instant t, le mobile se trouve à une certaine distance de l'origine O du repère donnée par :
b°) Vecteur vitesse moyenne d'un
mobile ponctuel :
Si, dans un référentiel donné, entre les dates t 1 et t3, le mobile se déplace de M1 en M3, alors le vecteur vitesse moyenne entre
ces deux dates est :
Vmoyenne=
=
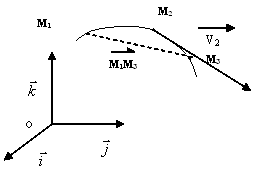
c°) Vecteur vitesse instantanée d'un mobile ponctuel :
Si, dans un référentiel donné, les dates t 1et t3 figurant dans l'expression précédente se rapprochent de plus en plus, on
montre, en mathématiques, que la limite du vecteur vitesse
moyenne est la dérivée par rapport au temps du vecteur position .
Cette limite est le vecteur vitesse instantanée au point M2 (à l'instant t2) :
V2=
Lim ()=
avec t1 t3
-le point d'application de V2 est le point M2 où se trouve le mobile ponctuel à cet instant (t2).
- la direction de V2 est celle de ………………………..en M2 à la trajectoire suivie par le point étudié.
- le sens du vecteur vitesse est celui du mouvement.
- la longueur de V2 représente, à une échelle donnée, la…………………… du vecteur vitesse à cet instant.
- Les coordonnées de V2 dans le repère orthonormé, sont données ci-dessous (III°) b°) :
- La vitesse s'exprime en ……………..dans le système international d'unités.
III°) Le Vecteur accélération d'un mobile ponctuel :
1°) Définitions : Dans un référentiel donné le vecteur vitesse d'un mobile ponctuel peut changer de valeur et (ou) de
direction. Ce changement éventuel peut se faire plus ou moins rapidement.
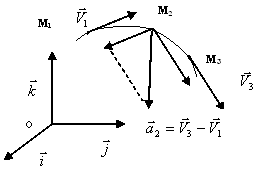
Par définition, on appelle vecteur accélération instantanée (par exemple au point M2) noté a2 la dérivée par rapport
au temps du
vecteur vitesse 
:
a2=
Lim (
)=
=
-
le point d'application de 
est le point où se trouve le mobile ponctuel à cet instant (M2)
-
le vecteur est dirigée vers …………………………….. de la trajectoire.
- la longueur de représente, à une échelle donnée, la norme du vecteur
accélération à cet instant. Elle se donne en
…………..
- Les coordonnées de dans le repère orthonormé , sont données ci-dessous.
2°) Coordonnées des vecteurs position, vitesse et accélération dans un
repère orthonormé :
Dans le repère , lié au référentiel d'étude, les coordonnées des vecteurs position , vitesse et accélération
d'un mobile ponctuel sont :
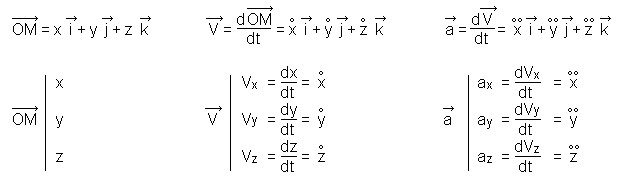
Remarque : Dans le cas d'un mobile non ponctuel (un solide, par exemple), chaque point possède sa propre trajectoire,
sa propre vitesse, sa propre accélération.
En classe terminale, on se limite souvent à l'étude du mouvement du centre d'inertie G du système.
3°) Représentations des vecteurs vitesses et accélérations pour une trajectoire rectiligne :
Place quelques vecteurs vitesses et accélérations dans chaque cas
Cas d’un mouvement rectiligne accéléré Cas d’un mouvement rectiligne uniforme Cas d’un mouvement rectiligne ralenti
IV°) Les lois de Newton :
1°) Première loi de Newton (Principe de l’inertie vu en seconde et 1°S) :
=
reste constant en direction, sens et norme
Remarques :
- Contrairement à ce que croyaient les anciens, un solide peut donc se déplacer bien que la somme des forces appliquées à ce solide
soit nulle. Le véritable opposition n'est pas entre mouvement et repos mais entre mouvement rectiligne uniforme (le repos n'est qu'un
cas particulier) et les autres types de mouvement. C'est un des mérites de Newton (1642-1727) d'avoir bien compris cela.
- Si la somme des forces extérieures appliquées à un solide est nulle on dit que ce solide est……………………….
- Un référentiel Galiléen est un référentiel dans lequel le principe de l’inertie est vérifié (ex : table d’une classe ,………….....................
...................................................................sont de bons référentiels galiléens pour des expériences de quelques minutes)
- Le référentiel Galiléen absolument parfait………………………..
2°) Deuxième loi de Newton :
En 1°S on a vu qu’une force (ou une somme
de forces) pouvait modifier le mouvement d’un système. On a vu que si
varie
alors la somme des forces extérieures appliquées au système était ………………………………… La direction et le sens de la
somme des forces extérieures étaient ceux de
la variation de
au cours de la durée
: 
=k
L’énoncé complet de cette 2ième loi de Newton (ou principe fondamental de la dynamique) vérifié dans le TP n°17 est :
Dans un référentiel Galiléen, la somme des forces extérieures appliquées à un solide est égale au produit de la masse m du solide
par
l'accélération 
de son centre d'inertie :
=m.
Remarque : Si = 
alors =
…………… et, par conséquent, 
reste
………………….. en direction, sens
et norme (on retrouve la ……………………….. loi de Newton).
3°) Troisième loi de Newton :
a°) Interaction de deux corps :
On dit que deux corps A et B sont en interaction si l'état de mouvement ou de repos de l'un (A) dépend de l'existence de l'autre (B).
Une interaction entre deux corps A et B suppose toujours deux actions réciproques : celle de ….. sur …… et celle de ……… sur
……….............................
b°) Troisième loi de Newton (Loi des
actions réciproques) :
A
/ B, l'autre exercée par B sur A, notée …………. Les deux forces associées à une
même interaction sont toujours égales et opposées :
A
/ B = ………………….
Exemple :
Interaction à distance Terre / Lune.
La Terre attire la
Lune avec une force 
.
Réciproquement, la Lune attire la Terre avec une force …………. égale et ………………… à :
