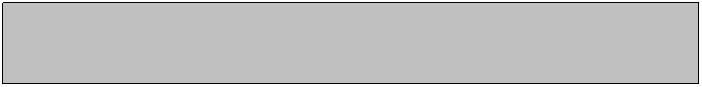Aux échelles
atomique et nucléaire, on préfère utiliser
l’unité de masse atomique notée u, dont
la valeur correspond au 1/12 de la masse d’un atome de carbone 12 (Z=6) :
1u =1,66054.10-27 kg
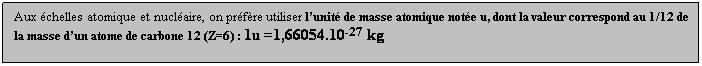
Noyaux, masse et énergie nucléaire
(chapitre 6 de physique)
Introduction : En France, la production de l’énergie électrique provient pour plus des trois quarts de l’énergie nucléaire.
Dans les réacteurs nucléaires, c’est la chaleur produite par la fission de l’uranium qui est utilisée. D’où provient cette énergie ?
I°) Aspect énergétique des réactions nucléaires :
1°) Perte de masse dans une réaction nucléaire :
Exercice 1 (réponses derrière la feuille) : Soit la désintégration a subie par un noyau de Po, dont l’équation bilan est :
226 …. 4
Ra ® Rn + He + g
88 86 ….
Données : (en unités de masse atomique u)
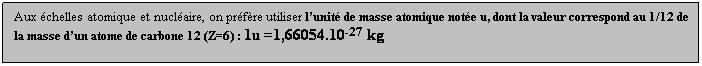
Questions :
1°) Quels sont les deux formes d’énergies libérées ?
2°) Complète l’équation bilan ci-dessus en justifiant.
3°) Calculer mavant – m après pour les noyaux lors de la réaction.

2°) Relation d’Einstein :
E0=m.c2
E0
s’exprime en ………. et m en kilogramme (kg)
c
est la vitesse de la lumière dans le vide qui vaut : c=………………….
Aux échelles atomique et nucléaire, on préfère exprimer les énergies en électronvolt (eV) ou en mégaélectronvolt (MeV) :
1eV==1,6022 .10-19 J et
1MeV=106 eV=1,6022.10-13 J

Exercice 2 : (réponses derrière la feuille) :
1°) Ecrire un bilan énergétique (en eV) pour l’équation du 1°) dans le cas où la particule de radium est au repos, le radon
et l’hélium étant en mouvement.
2°) En déduire l’expression de l’énergie libérée puis donner sa valeur.
3°) Energie de liaison d’un noyau :
Exercice 3 (réponse derrière la feuille) : Supposons possible le fractionnement d’un noyau d’ 4He en 2 protons et 2 neutrons).
Comparons la masse du noyau d’hélium au repos et la masse de ses nucléons (famille des protons + neutrons) séparés au repos.
Données : (en unités de masse atomique u) Masse d’un noyau d’4He=4,001 50 u ; Masse d’un proton =1,007 28 u;
Masse d’un neutron =1,008 66 u


Exercice 4 :
1°) Exprimer et calculer l’énergie correspond au défaut de masse de l’exercice 3 en eV.
2°) Représenter sur un diagramme énergétique l’énergie des nucléons séparés et celle du noyau.
![Zone de Texte: Définition : L’énergie de liaison El d’un noyau de masse m est l’énergie que le milieu extérieur doit …………. Pour
le séparer en ses Z protons de masse mp et ………. neutrons de masse mn. Elle vaut :
El= [Z.mp + (A-Z).mn-mnoyau].c2
Inversement lors de la formation d’un noyau, il y a …………………………………………… vers le milieu extérieur.](nrjnucleaire_fichiers/image007.gif)
4°) Energie de liaison par nucléon (courbe d’Aston):

Un noyau sera d’autant plus stable que l’énergie de liaison par nucléon sera plus ……………………. (voir courbe d’Aston p 115).
Les noyaux stables (environ 8 MeV par nucléon) sont des noyaux pour lesquels : …………..<A<…………………
Les noyaux instables : - A>190 ex : 235U peuvent se briser en 2 noyaux légers appartenant au domaine de stabilité , c’est de
a …………..
- A<20 :des noyaux très légers (comme les noyaux 1H) peuvent se fusionner pour donner un noyau plus
stable, c’est la réaction de …………………….
II°) Les réactions nucléaires provoquées :
1°) Les 2 types de réactions nucléaires provoquées :
Une réaction nucléaire est provoquée si elle est obtenue par choc d’une particule sur un noyau ou par choc de 2 noyaux.
Il existe deux types de réactions provoquées :
Remarque : Au cours des réactions nucléaires (spontanées ou provoquées) les lois de la physique sont vérifiées ,
en particulier conservation du nombre de charges électriques (Z) et du nombre de neutrons (N).
2°) La fission nucléaire : réaction présente dans les réacteurs nucléaires et dans la bombe A (HIROSHIMA).
Le phénomène de fission fut observé pour la première fois en 1938 par 2 allemands HAHN et STRASSMAN alors qu’ils bombardaient
de l’uranium par des neutrons. Cependant c’est Irène et Frédéric JOLIOT CURIE (prix Nobel de Chimie en 1935) qui en 1934
synthétisèrent les premiers isotopes artificiels.
Exercice 5 : Equilibre les équations suivantes traduisant la fission découverte par HAHN et STRASSMAN :
... 235 ... .... ...
n + U ® Sr + Xe + 2 n + g
... .... ..... ..... ....
... 235 ... .... ...
n + U ® La + Br + n
... .... ..... ..... . ....
La fission de 1 g d’isotope 235 de l’uranium (qui nécessite le traitement de 140 g d’uranium naturel) fournit ainsi une
énergie d’environ 80 GJ, ce qui correspondrait à la combustion d’environ 2 tonnes de pétrole.
3°) La fusion nucléaire :
Ces réactions sont à l’origine du rayonnement des étoiles et du soleil : l’énergie libérée est appelée énergie thermonucléaire.
L’homme sait initier (………………..) ces réactions mais il ne sait pas les contrôler , c’est le cas de la bombe H.
Exercice 6 : Equilibre les équations suivantes traduisant la fusion nucléaire dans le soleil :
2 2 3 ...
H + H ® H + H
.... .... ... ....
3 1 ... ...
H + H ® He + n
.... .... ... ....
2 3 ... ...
H + H ® He + n
.... .... ... ....
III°) Énergie libérée lors d’une réaction nucléaire :
Une réaction nucléaire fournit de l’énergie au milieu extérieur lorsqu’elle s’effectue avec ………………………………….