Les ondes mécaniques progressives et périodiques (chapitre 3
de physique)
Introduction : Une note de musique obtenue avec un diapason est une onde mécanique progressive périodique.
Comment caractériser ce type d’onde ?
I°) Définition :
|
Une onde mécanique
est progressive si elle se propage depuis un point source
dans ………………………..……..Elle est périodique si la
perturbation se ………………………….. de façon identique au ………………………………… ;
c’est un mouvement vibratoire entretenu
(vagues de la houle, la d’un diapason, ondes sur une cuve à onde….) |
II°) Onde mécanique périodique sinusoïdale :
a°) Périodicité temporelle (période) :
|
Définition:
La période d'un phénomène périodique est la durée au bout
de laquelle le phénomène se ………………….à lui-même. On la note T et elle
s'exprime en ……………….. (s).
Définition:
La fréquence d'un phénomène périodique représente le nombre de
phénomènes effectués par…………... On la note généralement f, son unité est
le………….. (…………………). La fréquence est l'inverse de la période :
|
Pour définir la période ou la fréquence d’une onde mécanique progressive sinusoïdale on utilise un stroboscope.
b°) Principe de la stroboscopie :
|
|
|
|
|
|
|
Soit Te la période des éclairs du stroboscope.
|
Remarques : - La valeur la plus ………………… de la période (ou la plus …….……… des fréquences) des éclairs qui
donne l'immobilité apparente
est égale à la période du
phénomène : T éclair= T phénomène périodique
- Quand T éclair< T phénomène
périodique alors le phénomène périodique va au ralenti ……………………………….
- Quand T éclair>T phénomène périodique alors le phénomène périodique va au ralenti ……………………………….
III°) Onde progressive périodique à une dimension:
1°) Etude expérimentale :
Soit une source S (extrémité d’une scie sauteuse) imposant une perturbation périodique sinusoïdale
au milieu de propagation (corde).
On constate qu'une onde progressive périodique se propage dans le milieu.
2°) Périodicité temporelle
|
|
Représentation spatiale de la corde |
|
|
Ci-joint (à droite) , l'aspect de la corde à un instant donné. L'élongation de la source et d'un point M quelconque est en général différente, mais on peut remarquer une périodicité dans le mouvement de chaque point de la corde. |
|
|
|
Représentation temporelle du point S |
Représentation temporelle du point M |
|
|
|
|
|
|
L'élongation de la source S est ………………………de période T. C'est une fonction sinusoïdale du temps. |
L'élongation du point M est elle aussi périodique de même période T. |
|
|
La période du mouvement de chaque point de la corde est imposée par la source S. |
||
3°)
Périodicité spatiale
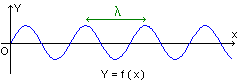
L'aspect de la corde à un instant donné est une fonction sinusoïdale de
l'abscisse x de chacun des points du milieu.
Définition:
On appelle longueur d'onde (notée l)
la période spatiale de l'onde
progressive périodique.
|
L'onde présente donc une double périodicité:
|
4°) Relation entre période et longueur d'onde
|
|
|
|
|||||||
|
|
|
La longueur d'onde est la distance parcourue par l'onde pendant une durée égale à
………………………..
Remarques : - l varie avec ………….……….si on garde le même milieu de propagation (donc même ………………..). - si on change de milieu de propagation (donc de ……… …………), pour la même fréquence, l ………….
|
Remarques:
 |
|
||
|
 |
|
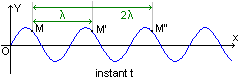
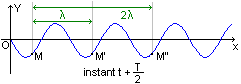
- Les points M, M' et
M'' conservent la même élongation quelque soit l'instant t. On dit que les
points M, M' et M'' vibrent en phase,
dans ce cas 2 points qui
vibrent en phase sont séparés par une distance
d= ………… (avec k entier
).
- Les points A et C
ainsi que B et C ont des
élongations opposées quelque soit l'instant t. On dit que les points A
et C ainsi que B et
C vibrent en ……………… de
phase,
dans ce cas 2 points qui vibrent en
…………..…… de phase sont séparés par une distance
d=
……………… (avec k entier ).
|
IV) Cas des ondes à deux ou à trois dimensions :
1°) Ondes à la surface de l'eau
|
|
|
|
Ondes circulaires |
|
|
|
|
|
Les points M1 et M2 vibrent en phase si |d2-d1| = kl. |
|
|
Ondes rectilignes |
|
|
|
Les points M1 et M2 vibrent en phase si d = ….. |
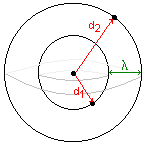2°) Ondes sonores
Les points M1 et M2 vibrent en phase si |d2-d1| = k.l (voir image ci-contre).
V°) Diffraction et dispersion :
1°) Diffraction d'une onde progressive sinusoïdale
Soit une onde plane périodique (réalisée avec une cuve à onde) rencontrant un obstacle ou une ouverture.
|
|
|
|
Cas n°1 |
Cas n°2 |
|
|
|
Dans le cas n°2, l'onde change de direction et de comportement sans changement de sa longueur d'onde: elle est
diffractée (le phénomène mis en évidence s'appelle la diffraction).
|
Définition :
Une ouverture (ou un obstacle)
interposé sur le trajet d’une onde progressive, se comporte comme une
source secondaire. Cette dernière émet dans toutes les directions,
et à la même fréquence que la source primaire (même longueur d’onde
, même ……………….) : c’est le phénomène de diffraction. Plus la
longueur de l’ouverture (a) se
rapproche de la longueur d’onde de la source
l,
plus ce phénomène sera …………………
|
2°) Dispersion d'une onde (activité réalisé à partir de clichés pris sur une cuve à onde) :
1°) Mesurer la longueur d’onde moyenne pour les 4 clichés.
2°) Calculer la vitesse correspondante dans chaque cas.
3°) Conclure
|
Définition:
Un milieu est dit dispersif si la célérité des ondes qui
se propagent dans ce milieu varie avec la …………………
|
L’eau est un milieu dispersif (voir activité ci-dessus). L’air n’est pas un milieu dispersif pour les ondes sonores.
Les aiguës (hautes fréquences) et les graves (………………………………………) parviennent simultanément à notre oreille.
Ce constat n’est plus vrai quand les amplitudes sonores sont très élevées : le roulement du tonnerre correspond à l’arrivée
tardive des basses fréquences (sons graves).
