Mesure de la pseudo période d’un pendule
à l’aide d’une Webcam et du Logiciel Avistep
Réalisation de sa propre vidéo :
· La Webcam doit être branchée sur le port USB de l’ordinateur.
· Il faut que l’ordinateur la reconnaisse (aller dans poste de travail et cliquer sur l’icône de la
Webcam PHILIPS SPC 900 NC).
· Ouvrir le logiciel de capture VLounge puis aller dans Préférences\ Dossier des médias\ et taper
D:\Données.
· Placer la Webcam sur l’unité central puis positionner le pendule sur la table d’en face.
· Mesurer la longueur totale de la tige verticale placée en face de votre Webcam (La tige doit
apparaître intégralement sur la vidéo) .
· Mesurer aussi la longueur de votre pendule (centre de la tige horizontale au centre de la boule).
· Écarter la boule associée à votre pendule d’un petit angle par rapport à la verticale (pas plus de 20°environ). Demander à votre binôme de démarrer la vidéo puis lâcher le pendule (pas plus de 10 s
d’acquisition).
· Il faut convertir le fichier MPEG en AVI grâce au logiciel VirtualDub présent dans ressources : S_option_SI\ sciences physiques\T°S (ouvrir la vidéo réalisée et présente dans données puis
l’enregistrer toujours dans Données en format AVI).
Exploitations
· Utiliser Avistep en fixant un repère et une échelle puis pointer les différentes positions prises par le pendule
au cours du temps.
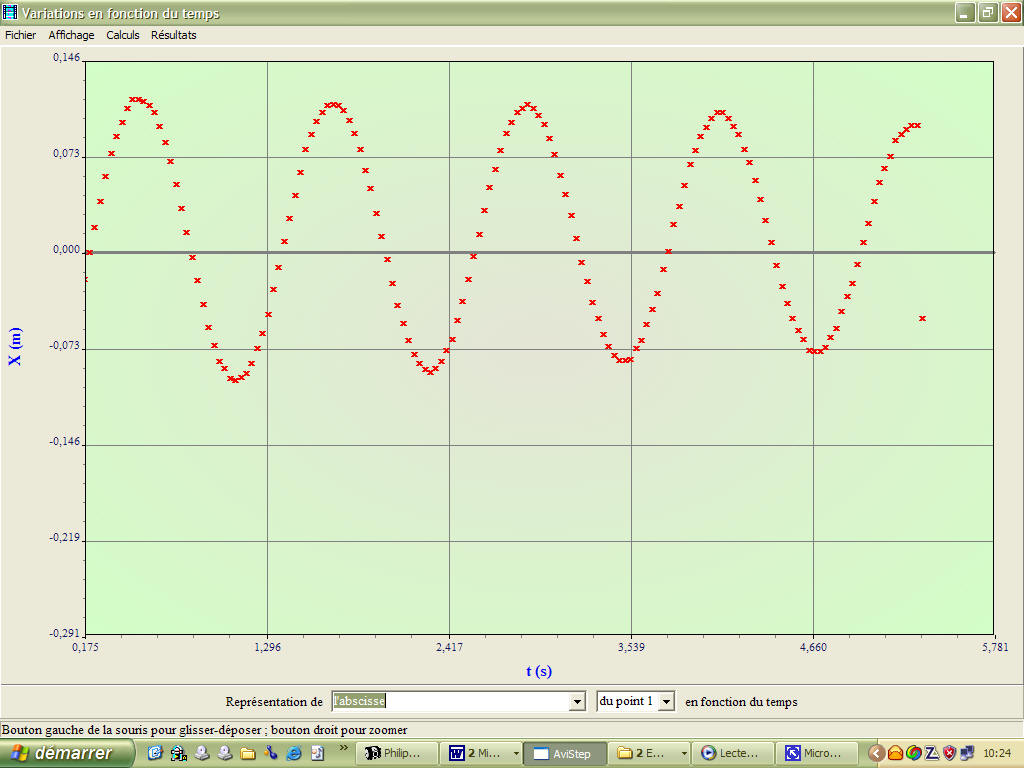
· Dans Résultats choisir Variations en fonction du temps puis visualiser x=f(t) puis répondre aux 3 questions suivantes :
Questions :
Q1 : Quelle type de fonction mathématique est associée à x=f(t).
Q2 : Trouver le plus précisément possible la valeur de la pseudo-pèriode, à partir de la courbe
x=f(t).
Q3 : Comparer la valeur obtenue précédemment à la valeur théorique (% d’erreur) puis commenter.
A La fin de cette activité n’oublier pas de supprimer tous vos fichiers vidéos
Résultat : Pour un pendule "maison" (yoyo de longueur environ 0,34 cm voir la vidéo en MPEG)
je trouve un temps de 4,749 spour 4 pseudo-pèriodes soit une pseudo-pèriode à environ 1,18 s. Par la
théorie on trouve T=2p(0,34/9.81)1/2 soit 1,17 s. La valeur expérimentale et théorique sont très proches
(1% d'erreur).
