Un
condensateur est constitué de deux conducteurs métalliques (les armatures) en
influence mutuelle, séparés par un isolant Le dipôle R,C (chapitre 7 de Physique)
Introduction : Juste avant l’éclair, la terre et les nuages qui la surplombent constituent un énorme condensateur.
La base du nuage est chargée négativement ; le sol en regard est chargé positivement. Qu’est-ce qu’un
condensateur ? Quels sont les mécanismes de charge et de décharge d’un condensateur ?
I°) Le condensateur :
Définition et symbole :
Un
condensateur est constitué de deux conducteurs métalliques (les armatures) en
influence mutuelle, séparés par un isolant
(le diélectrique). Le symbole du condensateur est :
On notera qu'un circuit (en courant continu) comportant un condensateur est un circuit ouvert. Il ne laisse donc pas passer un
courant permanent. Un condensateur se comporte comme un interrupteur ouvert une fois la charge terminée. Un condensateur
ne peut s'utiliser qu'en courant variable ou en régime transitoire.
II°) Lois de base :
1°) la loi d’ohm :
en courant continu :
……………………. U en V, R en ohm et i en A
en courant variable
C’est la même loi. Elle est valable à chaque instant, donc c’est une relation entre les grandeurs instantanées :
U(t)=R.i(t)
Si dans le circuit, il y a uniquement des résistances, alors elle s’applique aux grandeurs efficaces et maximales
grandeur efficace : mesurée avec le multimètre
grandeur max = amplitude mesurée avec l’oscilloscope
2°) Conventions générateurs et récepteurs :
Pour un dipôle générateur la flèche de la tension est dans le même sens que le courant.
Pour un dipôle récepteur la flèche de la tension est dans le sens inverse du courant.
|
UR |
|
I |
|
E |
|
R |
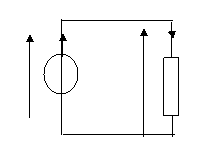
3°) Loi des mailles
|
UR1 |
|
I |
|
E |
|
R1 |
|
R2 |
|
UR2 |
Maille : chemin …………… d’un circuit.
Dans une maille la somme des tensions est égale à ……………. Il faut au préalable définir un sens de parcours de la maille.
Quand les flèches des tensions sont dans le même sens que le sens de parcours on met un ………. devant la tension.
Quand les flèches des tensions sont dans le sens inverse du sens de parcours on met un ………. devant la tension.
………. devant la tension.
Par exemple on a ………………………….=0V donc …………………………….
4°) L’intensité de courant i :
L’intensité i est la mesure du débit de charge, c’est à dire la quantité de charges q (en coulomb) qui traverse une section
S du
conducteur par unité de temps. Si ce débit de charge i est constant i=
(avec q en coulomb et t en seconde).
En régime variable , le débit de charge ou l’intensité ne reste pas constant. Dans ce cas l’intensité du courant à la date t est
définie par :
i(t)=
III°) Charge et décharge d’un condensateur (TP n°11) :
1°) Observations :
Expérience
|
E |
|
i |
|
éé |
|
éé |
Le courant passe dans le circuit puis ne passe plus : le condensateur est un dipôle qui accumule les ………… ,
les armatures emmagasinent des charges électriques ( bien remarquer qu’elles ne traversent pas l’isolant, les charges de
signe contraire apparaissent sur l’armature opposée car il y a conservation globale de la charge électrique).
Quand les armatures ont emmagasinées la quantité max de charges, il ne peut ……………………de courant électrique
car il y a la même quantité de charges sur l’armature reliée au pôle ……. et au pôle …….. le condensateur est chargé :
la tension aux bornes du condensateur …………………………………….aux bornes du générateur.
Au départ le condensateur était déchargé : UC …………………….
Nous allons mettre en évidence une grandeur qui va permettre de caractériser cette possibilité pour
le condensateur d’emmagasiner des charges électriques
2°) Capacité d’un condensateur :
Expérience : On utilise un générateur de courant constant avec i=0,1 mA
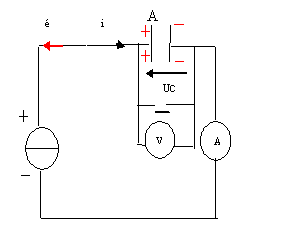
À l’aide d’un chronomètre et d’un voltmètre on mesure Uc = f(t)
Comme i = constant on peut
trouver q = i 
t
|
t (s) |
Uc (V) |
q
(C)=i |
q/Uc |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L'expérience montre qu'un condensateur soumis à une tension UC prend une charge q proportionnelle à UC telle que:
q = CUc
avec q: charge prise par le condensateur en coulomb (C)
Uc: tension électrique régnant aux bornes du condensateur en volt (V)
C: capacité du condensateur en farad (F)
Remarque : le farad est une unité représentant une très grande capacité, rarement rencontrée en électronique
ou au laboratoire. On utilise couramment les sous multiples: 1mF=10-3F, 1µF=…………., 1nF=…………… (nanofarad)
et 1pF=10-12F (picofarad).
IV°) Réponse d'un dipôle RC soumis à un échelon de tension (TP n°13) :
1°) préliminaire :
On dit qu'un dipôle est soumis à un échelon de tension si la tension électrique appliquée à ses bornes
passe brutalement (en une durée extrêmement brève) de ………… à une tension constante E. Ou inversement si
la tension électrique appliquée à ses bornes passe brutalement de la valeur ……….. à la valeur………………….
La réponse d'un dipôle RC soumis à un échelon de tension est le comportement électrique de ce dipôle. Ce comportement
peut être caractérisé par l'évolution de la tension aux bornes de ce dipôle, par l'évolution de ……………………………ou par
………………………………………………………………au cours du temps.
L'évolution de la tension aux bornes du dipôle ohmique ou aux bornes du condensateur peut être facilement visualisée à l'aide
d'un oscilloscope à mémoire (TP n°13) ou à l’aide d’un ordinateur muni d'une interface (voir TP N°11).
L'évolution de l'intensité du courant peut être visualisée à l’aide de la tension UR aux bornes du dipôle ohmique.
En tenant compte de la loi d'Ohm (UR (t)=Ri(t), on peut tracer la courbe i(t)=UR(t)/R.
L'évolution de la charge du condensateur est obtenue à l'aide de la formule q(t)=C UC(t).
voir photos du TP n°13
2°) Etude expérimentale (TP N°11+ 13) :
Lors du TP n°11 nous avons constaté que :
Ø Lors de la charge du condensateur, la tension aux bornes du condensateur …………plus ou moins rapidement
pour atteindre la valeur de la tension imposée par le …………………de tension constante E.
Ø Les paramètres qui ont une influence sur la rapidité de cette évolution sont: la ………………….du dipôle ohmique
et ……………………… condensateur. E n'a aucune influence sur cette rapidité d'évolution.
Ø Plus R est………………., plus UC met de temps pour tendre vers E.
Ø Plus C est…………………….., plus UC met de temps pour tendre vers E.
Ø La durée t=RC apparaît comme une durée caractéristique de l'évolution du système. t donne un ordre de grandeur du
temps que met la tension UC pour atteindre (à 63% près) la valeur E.
Lors du TP n°13 nous avons constaté que :
Ø Lors de la décharge du condensateur, la tension UC décroît plus ou moins rapidement de E à 0 V. On peut faire les mêmes observations qu'en ce qui concerne la charge.
Ø La tension UC est une fonction ……………………. du temps pour un cycle charge-décharge.
Ø La tension UR aux bornes du dipôle ohmique est une fonction ………………….. du temps pour un cycle
charge-décharge. Il en est donc de même pour i.
3°) Etude théorique :
a°) Etude théorique de la charge d'un condensateur :
On cherche à retrouver les résultats expérimentaux en utilisant les lois d'électricité du circuit.
* On cherche l'équation différentielle vérifiée par la tension uC :
|
UC >0 |
|
I>0 |
|
I’<0 |
|
R |
|
UR >0 |
|
E>0
|
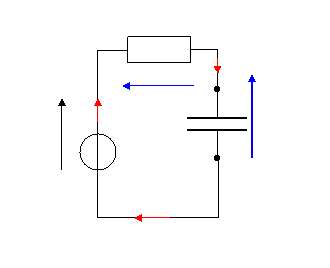
* Loi des mailles avec les conventions récepteurs
pour la résistance et le condensateur
: uR + uC = E
Loi d'Ohm pour la résistance : uR = R . i
* D'après les relations : i = dq / dt et q = C.uC on a dq/dt = C.duC/dt (car C est une constante)
ce qui implique uR = R.C.duC/dt.
L'équation différentielle en charge est : R.C.duC/dt + uC = E (1)
* Solution de l'équation différentielle précédente :
On ne cherche pas de résoudre ces équations différentielles (trouver la fonction uC = f(t) vérifiant l'équation) mais à
vérifier que la fonction uC = a.e -t/ t+ b (où a, b et t sont des constantes) est bien solution de l'équation différentielle.
duC/dt = - (a/t).e-t/t.
L'équation différentielle (1) devient : - R.C.(a/t)
.e-t/t + a.e-t/t
+ b = E
soit
a.e-t/t.( 1 – R.C / t) + b = E
Cette équation est vérifiée quelque soit la date t si : b = E et 1- R.C / t = 0 donc si t= R.C
(car b et E sont des constantes et e-t/t est variable)
On a donc : uC = a.e-t/RC + E
Pour déterminer a, on utilise la valeur de uC à l'instant t = 0 s.
A t = 0 s, uC
= 0 V alors 0 = a + E => a = -E.
Solution de l'équation différentielle lors de la charge : uC = E.( 1- e-t/RC).
b°) Etude théorique de la décharge d'un condensateur : (avec un signal rectangulaire on a E=0 V comme s'il n'y
avait plus de générateur)
|
UC >0 |
|
I’<0 |
|
I’<0 |
|
R |
|
UR <0 |
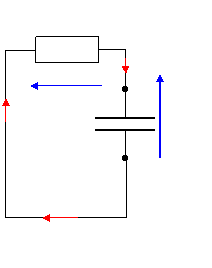
* Loi des mailles uR + uC = 0 (si on garde le même sens du courant I' est négatif , ce qui revient à mettre un
I'' en sens inverse mais dans ce cas I'' sera positif : ce qui est cohérent avec le fait que le condensateur se
comporte comme un générateur en décharge).
D'après les relations : uR = R . i , i = dq / dt
ainsi que q = C.uC on a de
nouveau dq/dt = C.duC/dt
ce qui implique uR = R.C.duC/dt.
L'équation différentielle associée à la décharge est : R.C.duC/dt + uC = 0 (2)
* Solution de l'équation différentielle précédente :
On cherche de nouveau à montrer que la fonction uC = a.e -t/ t + b (où a, b et t sont des constantes) est solution
de l'équation différentielle.
duC/dt = - (a/t).e-t/t.
L'équation différentielle (2) devient : - R.C.(a/t)
.e-t/t + a.e-t/t+ b = 0
soit a.e-t/t.( 1 – R.C /
t) + b = 0
Cette équation est vérifiée quelque soit la date t si : b = 0 et 1- R.C / t = 0 donc t= R.C
On a donc : uC = a.e-t/RC
Pour déterminer a, on utilise la valeur de uC à l'instant t = 0 s
(début de la décharge)
A t = 0 s, uC = E (début de la décharge) alors a = E.
Solution de l'équation différentielle lors de la charge : uC = E.e-t/RC .
4 ) Etude de l'intensité dans chaque phase :
On peut faire la même démarche que précédemment en cherchant l'intensité :
Dans les deux cas (charge ou décharge), d'après la loi d'Ohm on a : i = uR/ R
* Cas de la charge : uR = E - uC ; i = (E - uC ) / R = (E – E + E.e –t/ RC)/ R = (E / R).e –t/ RC =i
L'intensité du courant de charge décroît aux cours de la charge, de la valeur i0 = E / R à une valeur proche de 0.
Plus la phase de charge avance, plus il est difficile de charger le condensateur.
* Cas de la décharge.: uR = - uC donc i = - uC / R = - E.e -t / RC / R =i
Le courant circule dans le sens inverse (ou dans le même sens mais de signe négatif) et croît de la valeur
i0 = -E / R à une valeur proche de 0.
Conclusion : Entre la phase de charge et le début de la décharge il y a discontinuité du courant.
5) La constante de temps t du dipôle RC :
a°) Dimension de t
[RC] = [R].[C] or R = U / I donc [R] = [U].[I]-1 (1)
C = q / u donc [C] = [Q]/[U] soit [C] = [I].[t]/[U] (2)
Multiplions (1) par (2) [RC]=[U].[I]-1.[I].[t].[U]-1 d'où [RC] =[t]
t = R.C a la dimension d'une durée, est appelé constante de temps du dipôle RC et s'exprime en seconde
(si R est en ohm (W) et C en farad (F)).
b°) Détermination expérimentale de t :
En charge :
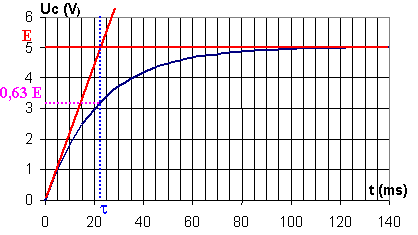
Quand t=t =RC lors de la charge on a uC = E.( 1- e-RC/RC)=E. (1-1/e)=0,63E=63 % E
On peut déterminer t par la méthode de la tangente à l'origine (moins précis que la méthode des 63 %) :
t est le temps où la tangente à l'origine coupe l'asymptote horizontale (u = E).
En décharge :
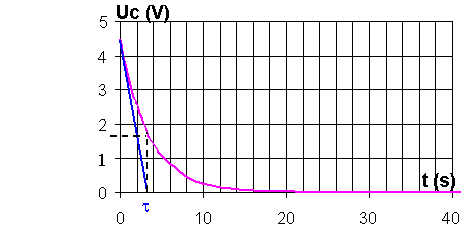
Quand t=t =RC lors de la décharge on a uC = E.e-RC/RC =E.1/e=0,37E=37 %E
Méthode de la tangente à l'origine (l'origine correspondant au début de la
décharge) :
t temps où la tangente à l'origine coupe
l'asymptote horizontale (u = 0).
|
37%E
soit
37%4 ,5 |
V°) Energie emmagasinée dans un condensateur :
Un condensateur emmagasine de l'énergie lorsqu'on le charge. Cette énergie est restituée lors de la décharge
de ce même condensateur. Nous admettrons que l'énergie d'un condensateur chargé est donné par la relation :
E =
C UC² D'après la relation q = C . UC , on peut aussi écrire :
E =
Bien entendu l'énergie est donnée en Joules
